1.3. Образование коллоидных систем при конденсации (кристаллизации) из растворов или расплавов

Образование коллоидных систем из растворов или расплавов путем конденсации играет важную роль в технологической практике текстильного производства, синтеза полимеров путем эмульсионной полимеризации, при формировании волокон из растворов или расплавов полимеров. Особенно часто используют дисперсии (золи) кремнезема, гидроксидов алюминия, кальция или железа для очистки сточных вод текстильного производства от красителей и текстильно-вспомогательных веществ.

Рассматривая процесс конденсации из паровой фазы, можно получить уравнение, аналогичное уравнению (2.1.24) для свободной энергии образования критического зародыша при конденсации из раствора,

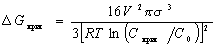, (2.1.25)

где С_крит , С₀ – концентрация насыщения раствора соответственно при формовании зародышей сферической формы и над плоской бесконечно протяженной макрофазой.

Рассматривая равновесие между распределенными в водной среде кристаллами различного размера (для сферических частиц - радиуса r) и бесконечно протяженной макрофазой следует учитывать, что вещество в частице обладает некоторым избытком свободной энергии по сравнению с бесконечно протяженной фазой, т.е. по аналогии с уравнением (2.1.14) для раствора можем записать

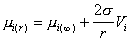, (2.1.26)

где V_i– молярный объем i-того компонента системы в конденсированном (твердом) состоянии.

В предположении идеальности растворов для любого из компонентов

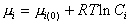. (2.1.27)

Для веществ в дисперсном состоянии

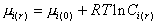. (2.1.28)

В бесконечно протяженной фазе

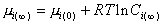, (2.1.29)

где 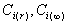– концентрации растворов, равновесно насыщенных по отношению соответственно к частицам радиуса r и к макрофазе.

Пересыщение раствора относительно равновесной концентрации образования бесконечно протяженной макрофазы может быть достигнуто путем резкого охлаждения раствора или изменения растворимости путем замены части воды другим растворителем.

При равновесии системы

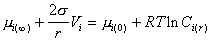. (2.1.30)

Учитывая уравнение (2.1.29),

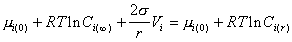, (2.1.31)

откуда

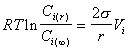(2.1.32)

или, опуская индекс i , получаем

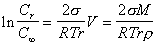, (2.1.33)

где r, М - соответственно плотность и молекулярная масса вещества в частицах.

Уравнение (2.1.33) известно как уравнение Оствальда-Фрейндлиха. Это уравнение часто используют для определения поверхностного натяжения твердой поверхности частиц при измеренных плотности, радиусе частиц и равновесной концентрации раствора. Найденные различными учеными значения поверхностного натяжения одних и тех же твердых кристаллических веществ подчас различаются на 1-2 порядка, что связано с приближенным характером уравнения (2.1.33) для кристаллических веществ, так как образование и рост кристаллов существенно отличаются от образования и роста капель жидкости, хотя при выводе уравнения (2.1.33) использовались представления, аналогичные тем, которые привлекаются к описанию процесса конденсации из паровой фазы. Тем более это уравнение дает высокую погрешность в системах, где кристаллы образованы из ионов, на поверхности которых формируется заряд. Вместе с тем уравнения (2.1.25) и (2.1.33) могут использоваться для приближенных расчетов, особенно при проведении серий экспериментов.

Учет электролитической диссоциации растворенного вещества проводится путем введения в уравнение Оствальда-Фрейндлиха степени диссоциации a или изотонического коэффициента i. Тогда уравнение (2.1.33) принимает вид

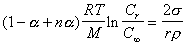, (2.1.34)

или

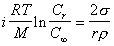, (2.1.34а)

где n – число ионов, на которые распадается молекула при диссоциации, i = (1 - a + na).

При равновесии в растворе сферических частиц различного радиуса уравнение Оствальда-Фрейндлиха принимает вид

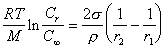. (2.1.35)

При отклонении формы частиц от сферической расчет проводят по уравнению Гросса

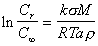, (2.1.36)

где k – коэффициент формы поверхности частиц; a – характерный линейный размер частиц.

Различная способность к растворению частиц разного размера в полидисперсных системах приводит к тому, что при длительном выдерживании мелкие частицы будут растворяться, а большие частицы расти далее за счет переноса вещества от малых частиц к большим через раствор. Такой процесс носит название «перекристаллизация» и именно он определяет седиментационную устойчивость коллоидных систем при хранении. Полидисперсность коллоидных систем в водной среде делает их принципиально неустойчивыми.

При получении коллоидных систем путем конденсации из расплава невозможно применение представлений о процессе зарождения новой фазы, использованных выше при рассмотрении конденсации из паровой фазы или из раствора. Кристаллические зародыши новой фазы в таких системах образуются при переохлаждении системы (расплава).

Учитывая уравнение Гиббса-Гельмгольца для температурной зависимости химического потенциала для переохлаждения расплава,

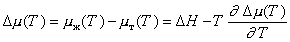. (2.1.37)

Так как

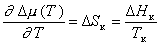, (2.1.38)

то

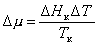, (2.1.39)

где индекс «к»обозначает конденсацию, DТ = Т_к-Т > 0 – переохлаждение.

Подставляя в уравнение (2.1.20) выражение (2.1.39), получаем уравнение для радиуса критического зародыша при формировании новой фазы из расплава

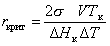. (2.1.40)

Из уравнения (2.1.40) следует, что чем больше переохлаждение расплава, тем меньше радиус кристаллического зародыша. Энергия Гиббса образования кристаллического зародыша в расплаве может быть рассчитана из уравнения, которое получается путем подстановки уравнения (2.1.39) в уравнение (2.1.24):

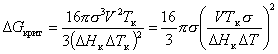, (2.1.41)

где V – молярный объем твердого вещества.