ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ,
ф-ции параметров состояния макроскопич. системы (т-ры Т, давления
р, объема V, энтропии S, чисел молей компонентов ni,
хим. потенциалов компонентов m, и др.), применяемые гл. обр. для описания
термодинамического равновесия. Каждому термодинамическому потенциалу соответствует набор параметров
состояния, наз. естественными переменными.
Важнейшие термодинамические потенциалы: внутренняя
энергия U (естественные переменные S, V, ni); энтальпия
Н= U — (— pV) (естественные переменные S, p, ni);
энергия Гельмгольца (свободная энергия Гельмгольца, ф-ция Гельмгольца) F
= = U — TS (естественные переменные V, Т, ni);
энергия Гиббса (своб. энергия Гиббса, ф-ция Гиббса) G=U — — TS — (— pV)
(естественные переменные p, Т, ni); большой термодинамич.
потенциал(естественные
переменные V, Т, mi).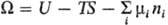
Термодинамические потенциалы могут быть представлены
общей ф-лой
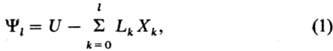
где Lk
- интенсивные параметры, не зависящие от массы системы (таковы Т, p, mi),
Xk-экстенсивные параметры, пропорциональные массе системы
(V, S, ni). Индекс l = 0 для внутренней энергии
U, 1-для H и F, 2-для G и W. Термодинамические потенциалы являются
ф-циями состояния термодинамической системы, т.е. их изменение в любом процессе
перехода между двумя состояниями определяется лишь начальным и конечным состояниями
и не зависит от пути перехода. Полные дифференциалы термодинамических потенциалов имеют вид:
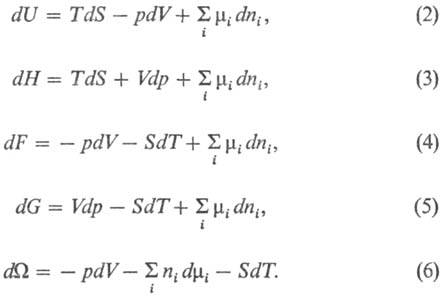
Ур-ние (2) наз. фундаментальным
ур-нием Гиббса в энергетич. выражении. Все термодинамические потенциалы имеют размерность энергии.
Условия равновесия термодинамич.
системы формулируются как равенство нулю полных дифференциалов термодинамических потенциалов при постоянстве
соответствующих естественных переменных:
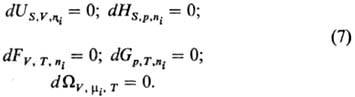
Термодинамич. устойчивость
системы выражается неравенствами:
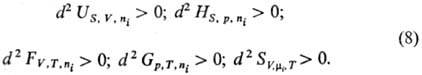
Убыль термодинамических потенциалов в равновесном
процессе при постоянстве естественных переменных равна максимальной полезной
работе процесса А:
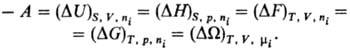
При этом работа А производится
против любой обобщенной силы Lk, действующей на систему, кроме
внеш. давления (см. Максимальная работа реакции).
Термодинамические потенциалы, взятые как ф-ции
своих естественных переменных, являются характеристическими ф-циями системы.
Это означает, что любое термодинамич. св-во (сжимаемость, теплоемкость и т.
п.) м. б. выражено соотношением, включающим только данный термодинамический потенциал, его естественные
переменные и производные термодинамических потенциалов разных порядков по естественным переменным. В
частности, с помощью термодинамических потенциалов можно получить уравнения состояния системы.
Важными св-вами обладают
производные термодинамических потенциалов. Первые частные производные по естественным экстенсивным переменным
равны интенсивным переменным, напр.:
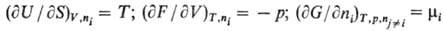
[в общем виде: (9Yl/9Хi)
= Li]. И наоборот, производные по естественным интенсивным переменным
равны экстенсивным переменным, напр.:
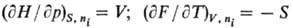
[в общем виде: (9Yl/9Li)
= Xi]. Вторые частные производные по естественным переменным
определяют мех. и тер-мич. св-ва системы, напр.:
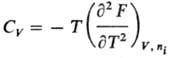
Т.к. дифференциалы термодинамических потенциалов
являются полными, перекрестные вторые частные производные термодинамических потенциалов равны, напр.
для G(T, p, ni):
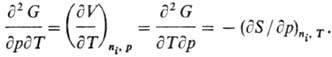
Соотношения этого типа
называются соотношениями Максвелла.
Термодинамические потенциалы можно представить
и как ф-ции переменных, отличных от естественных, напр. G(T, V,
ni), однако в этом случае св-ва термодинамических потенциалов как характеристич. ф-ции
будут потеряны. Помимо термодинамических потенциалов характеристич. ф-циями являются энтропия S (естественные
переменные U, V, ni), ф-ция Массье Ф1 =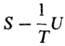 (естественные переменные 1/Т, V, ni), ф-ция
Планка
(естественные переменные 1/Т, V, ni), ф-ция
Планка 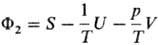 (естественные
переменные 1/Т, p/Т,
ni).
(естественные
переменные 1/Т, p/Т,
ni).
Термодинамические потенциалы связаны между собой
ур-ниями Гиббса-Гельмгольца. Напр., для H и G
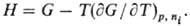
В общем виде:
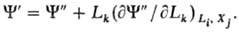
Термодинамические потенциалы являются однородными
ф-циями первой степени своих естественных экстенсивных переменных. Напр., с
ростом энтропии S или числа молей ni пропорционально
увеличивается и энтальпия Н. Согласно теореме Эйлера, однородность термодинамических потенциалов
приводит к соотношениям типа:
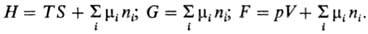
В хим. термодинамике, помимо
термодинамических потенциалов, записанных для системы в целом, широко используют среднемолярные (удельные)
величины (напр.,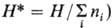 ,
парциальные молярные
величины [напр., стандартные изменения
термодинамических потенциалов в к.-л. процессе.
,
парциальные молярные
величины [напр., стандартные изменения
термодинамических потенциалов в к.-л. процессе.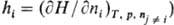 напр.,
стандартное изменение энтальпии при хим. р-ции равно разности энтальпий продуктов
и исходных в-в, когда и те и другие находятся при заданных
(выбранных) условиях, чаще всего при определенном внеш. давлении. Важные стандартные
величины-стандартные энтальпии образования хим. соед.
напр.,
стандартное изменение энтальпии при хим. р-ции равно разности энтальпий продуктов
и исходных в-в, когда и те и другие находятся при заданных
(выбранных) условиях, чаще всего при определенном внеш. давлении. Важные стандартные
величины-стандартные энтальпии образования хим. соед.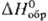 ,
энергии Гиббса образования хим. соед.
,
энергии Гиббса образования хим. соед. 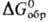 и т.п.
и т.п.
В статистической термодинамике
пользуются аналогами энергии Гельмгольца и большого термодинамич. потенциала,
к-рым отвечают соответственно канонич. и макрокано-нич. распределения Гиббса.
Это позволяет рассчитывать термодинамические потенциалы для модельных систем (идеальный газ, идеальный
р-р) по молекулярным постоянным в-ва, характеризующим равновесную ядерную конфигурацию
(межъядерные расстояния, валентные и торсионные углы, частоты колебаний и т.
п.), к-рые м. б. получены из спектроскопич. и др. данных. Возможен расчет термодинамических потенциалов
через сумму по состояниям Z (интеграл по состояниям). Подобный подход позволяет
установить связь термодинамических потенциалов с молекулярными постоянными в-ва. Вычисление суммы (интеграла)
Z для реальных систем-весьма сложная задача, обычно статистич. расчеты
применяют для определения термодинамических потенциалов идеальных газов.
Лит.: Кричевский
И. Р., Понятия и основы термодинамики, М., 1962; Мюнстер А., Химическая термодинамика,
пер. с нем., М., 1971.
М. В. Коробов.