1.3.3.Цилиндрические мениски
Если твердая пластинка погружена в жидкость так, как показано на рис. 1.7,б, то жидкость образует около пластинки мениск, форма которого может быть описана уравнением Лапласа (1.1.37).
При равновесии сила F уравновешивает не только вес пластинки, но и капиллярные силы, втягивающие пластинку внутрь жидкости (см. рис. 1.7,б). В точке y, взятой произвольно на прилегающем к пластинке мениске на высоте z от уровня окружающей жидкости, в гравитационном поле
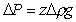. (1.1.48)
В любой точке внутри мениска на высоте z это давление будет одинаковым, а по высоте мениска оно возрастает от P0 до Pz. При совместном решении уравнений (1.1.37) и (1.1.48) получаем
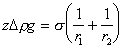. (1.1.49)
Уравнение (1.1.49) показывает взаимосвязь формы мениска и высоты z, однако этого оказывается не достаточно для определения формы мениска, так как оно не позволяет определить zmax=h, т.е. максимальную высоту, на которой жидкость ещё может контактировать с пластинкой.
Рэлей при рассмотрении случая контакта жидкости и прямой стенки получил двумерное решение для координаты точки y, для решения которого необходимо измерить краевой угол смачивания. Для определения координат необходимо решить два уравнения
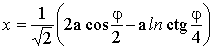(1.1.50)
и
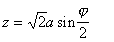, (1.1.51)
где x и z -горизонтальная и вертикальная координаты выбранной точки, соответственно; a - капиллярная постоянная.
По уравнению Рэлея нельзя правильно найти начало координаты x, которое в соответствии с уравнением(1.1.50) должно быть пр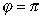и 
и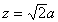 
, что лишено практического смысла.
Объем жидкости, удерживаемый единицей длины цилиндрического мениска, может быть найден на основании элементарного объема dV, который удерживается капиллярными силами на элементе поверхности dA радиусом кривизны r1[второй радиус кривизны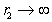 
, поэтому вторым слагаемым в скобках уравнения (1.1.37) можно пренебречь]:
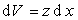. (1.1.52)
Из уравнения Лапласа (1.1.37) следует
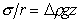(1.1.53)
и
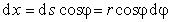. (1.1.54)
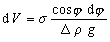. (1.1.55)
Интегрирование уравнения (1.1.55) при граничном условии, что при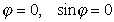 
и V=0 приводит к выражению
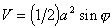. (1.1.56)
Уравнение (1.1.56) используется для расчета поверхностного натяжения при методе взвешивания пластинки (метод Вильгельми).