2.1.2. Микроскопия

Микроскопическое определение гранулометрического состава порошков и капель эмульсии представляет собой один из наиболее традиционных методов анализа. Метод с использованием оптического микроскопа ограничен размером частиц 5·10^-7 м в связи с тем, что меньшие частицы уже не отражают свет. Электронный микроскоп применяют для частиц размером 10^-9-10^-5 м. Более крупные частицы измеряют с помощью оптического микроскопа. Обычно для проведения микроанализа пробу исследуемого порошка диспергируют в хорошо смачивающей жидкости с добавками ПАВ. Диспергированный таким образом порошок помещают на предметное стекло и измеряют размеры частиц с помощью окулярной сетки или шкалы. Обычно измеряют все частицы, находящиеся в поле зрения. Число измеренных частиц определяется заданной точностью анализа. Очевидно, что чем больше охарактеризовано частиц, тем точнее результат.

Точность микроскопического анализа зависит от двух факторов: один из них - субъективные ошибки, другой обусловлен статистическим характером измерений. Достаточная точность измерений достигается при подсчете размера около 1000 частиц каждой фракции. Поэтому точность определения размера крупных частиц, которых обычно мало в поле микроскопа, как правило, невелика. В тоже время, если частицы имеют размер на границе разрешающей способности микроскопа или даже за нею, то определить их размер, а тем более содержание, практически невозможно. Для анализа дисперсий с частицами таких размеров применяют электронный микроскоп.

Одним из источников погрешностей при определении размеров частиц может быть их неправильная геометрическая форма. Обычно размер частиц определяют ее диаметром. Это справедливо, например, для капель эмульсии или для частиц латексов, которые имеют правильную сферическую форму. В этом случае диаметр частицы (капли) точно характеризует все остальные параметры: объем, поверхность, удельную поверхность. Если же частицы имеют какую-либо иную форму, то определение их «диаметров» затруднено. Действительно, какой же ее размер считать эквивалентным диаметру: ребро куба, диагональ грани или куба? Если же частицы имеют совсем уж неправильную форму, то характеризовать ее с помощью диаметра почти невозможно. Поэтому говорят о некотором эффективном диаметре, т.е. о диаметре такой сферической частицы, которая имеет одинаковый объем (поверхность и т.д.) с реальной частицей.

Микроскопический метод позволяет непосредственно видеть форму частиц, что также является положительной чертой этого метода.

В электронной микроскопии для оттенения формы и получения объемных характеристик частиц на препараты наносят пары тяжелых металлов или используют сканирующие приборы. Точность измерения повышается при использовании проецирующих микроскопов или приборов с телевизионной приставкой. Высокая точность подсчета характерна для микроскопов с автоматическим измерением числа частиц и их размера. Такие приборы в настоящее время не являются дефицитными.

Результаты подсчета числа частиц и определения их размера выражают в виде некоторой средней величины, в качестве которой наиболее часто используют

средний арифметический диаметр частиц или капель эмульсии

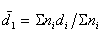, (2.2.1)

где d_i– средний диаметр чаcтиц в интервале числа частиц n_i; S n – общее число подсчитанных частиц;

средний квадратичный (средний по поверхности) размер частиц

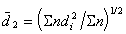, (2.2.2)

средний кубичный (средний по объему или массе) размер частиц

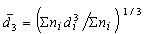. (2.2.3)

Для наиболее полной характеристики дисперсных систем используют распределение частиц по размерам в дифференциальной или интегральной формах. Для этого переходят от числа частиц каждой формы к их массе. Если частицы имеют правильную сферическую форму, то для массы всех частиц фракции 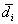(от d₁ до d₂, где d₁ – наименьший диаметр внутри фракции, d₂ – наибольший), можем записать

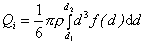, (2.2.4)

где r – плотность вещества частиц; f(d) = dN/dx – функция распределения числа частиц по размерам.

Полагая, что в узком интервале размеров частиц распределение равномерное, т.е.

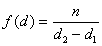. (2.2.5)

где n – число частиц в интервале размеров d₁< d < d₂, можем рассчитать массу всех частиц в этом узком интервале

. (2.2.6)

Общая масса всех частиц в исследуемом образце в интервале размеров от d_min до d_max составит

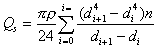. (2.2.7)

После расчета масс каждой фракции результаты выражают в виде таблиц или графиков

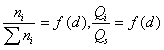. (2.2.8)