Дисперсионное взаимодействие

ДИСПЕРСИОННОЕ ВЗАИМОДЕЙСТВИЕ, составляющая межмолекулярного взаимодействия, определяемая квантовомех. флуктуациями электронной плотности частиц (молекул, атомов). Мгновенное распределение электрич. заряда молекулы, к-рому отвечает мгновенный дипольный момент молекулы (или более высокого порядка мультипольный момент), индуцирует электрич. мультипольные моменты в др. молекуле. Энергия взаимод. этих мгновенных мультипольных моментов и есть энергия дисперсионного взаимодействия Е_дисп. Дисперсионное взаимодействие между молекулами (атомами), находящимися в основных квантовых состояниях, всегда приводит к их притяжению. Энергию Е_дисп обычно представляют в виде разложения в ряд по обратным степеням расстояния R между молекулами: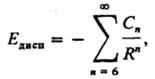

где С_n- коэф. разложения, n - целое число (n / 6). При больших R осн. вклад в значение Е_дисп дает диполь-дипольный член разложения —C₆/R⁶. Значение С₆ определяется через динамические поляризуемости a^А и a^B взаимодействующих молекул А и В. Точное выражение для С₆ представляет собой интеграл от произведения поляризуемостей, зависящих от мнимого аргумента iw:

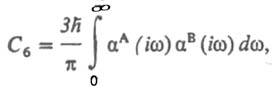
где h - постоянная Планка. Поскольку дисперсия света в в-ве также определяется в конечном счете поляризуемостью молекул в-ва, рассматриваемый вид межмолекулярного взаимод. получил назв. дисперсионного. Для качеств. оценок Е_дисп м. б. использованы приближенные ф-лы. Наиб. распространенные из них - ф-ла Лондона:

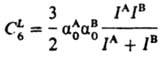
и ф-ла Слейтера-Кирквуда (Слэтера-Кирквуда):

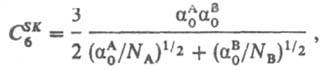
где a₀^A, a₀^B- статич. поляризуемости, I^А, I^B- первые потенциалы ионизации, N_A, N_B- число валентных электронов во взаимодействующих молекулах соответственно.

Ф-ла Лондона дает, как правило, для С₆ оценки снизу, ф-ла Слейтера - Кирквуда - сверху. Дисперсионное взаимодействие имеет место между всеми молекулами, независимо от наличия у них мультиполъных моментов. Для неполярных молекул, а также для молекул с небольшими дипольными моментами (СО, HI, НВr и др.) силы притяжения определяются в основном дисперсионным взаимодействием. Именно oно ответственно за притяжение между атомами инертных газов на больших расстояниях. Дисперсионное взаимодействие обусловлено корреляцией между флуктуациями дипольных моментов взаимодействующих систем; при этом среднее значение флуктуирующего дипольного момента м. б. равно нулю. Зависимость Е_дисп от R^-⁶ справедлива при условии, что электрич. заряды взаимодействуют мгновенно. При расстояниях между молекулами а 100 нм необходимо учитывать запаздывание, связанное с тем, что скорость света с имеет конечное значение. Электромагнитное поле мгновенного дипольного момента

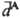молекулы А "достигает" молекулу В за время R/c и индуцирует в ней дипольный момент

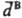, к-рый взаимодействует с

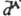по прошествии времени 2R/c после его образования. За это время

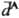может измениться. В результате величина запаздывающего взаимод. меньше величины мгновенного, что отражается в более крутом спаде кривой зависимости энергии запаздывающего дисперсионного взаимодействия от расстояния R. Для запаздывающего дисперсионного взаимодействия справедлива асимптотич. ф-ла Казимира-Полдера: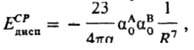

где a =¹/₁₃₇ - постоянная тонкой структуры (см. Спин-орбитальное взаимодействие). Учет запаздывания важен, напр., в теории коагуляции коллоидных систем. Дисперсионное взаимодействие ответственно за силы взаимод., возникающие при сближении и макроскопич. тел (Е. М. Лифшиц, 1955). В этом случае к появлению дисперсионного взаимодействия приводят флуктуации электромагнитного поля макроскопич. тела. Зависимость энергии дисперсионного взаимодействия от расстояния R между телами будет иной, чем в случае взаимод. изолированных частиц, и определяется формой тел. Так, для двух плоских пластин энергия запаздывающего дисперсионного взаимодействия зависит от R^-³, для двух параллельных цилиндров - от R^-⁶, для шариков - от R^-⁷. Эти зависимости получили эксперим. подтверждение.

Каплан И. Г., Введение в теорию межмолекулярных взаимодействий, М., 1982; Бараш Ю. С, Гинзбург В. Л., "Успехи физич. наук", 1984, т. 143, в. 2, с. 345; Молекулярные взаимодействия, пер. с англ., под ред. А. М. Бродского, М., 1984. И. Г. Каплан.

Ещё по теме

Межмолекулярное взаимодействие — природа и типы

Межмолекулярные взаимодействия в конденсированных фазах

Молекулярные силы в жидкостях

Спин-орбитальное взаимодействие в квантовой физике

Спин-спиновое взаимодействие в квантовых системах

Диффузия в коллоидных системах

Сопряжение связей в химии — особенности и влияние на реакции

Поверхностное натяжение и адсорбция в гетерогенных системах

Дисперсионное взаимодействие в жидкостях и полимерах

Электронный парамагнитный резонанс — принципы и применение

Электрокинетические явления — механизмы и применение

Поляризуемость частиц — свойства и применение

Свойства и применение смесей полимеров

Фарадеевский эффект — принципы и применение