Тепловая теорема
ТЕПЛОВАЯ ТЕОРЕМА (третье начало термодинамики), фундаментальное утверждение термодинамики, согласно к-рому в любых изотермич. процессах, протекающих вблизи абс. нуля т-ры, изменения энтропии системы не происходит, т. е.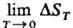 
= 0. Энтропия конденсйр. фаз при Т:0 не зависит от параметров состояния системы (давления, объема, напряженности магн. поля, поверхностного натяжения на границе раздела фаз и т. п.). Тепловая теорема не является следствием первого и второго начал термодинамики, имеет многочисл. эксперим. подтверждения и наз. третьим началом термодинамики. Впервые сформулирована В. Нернстом в 1906.
Важнейшими примерами соотношений, устанавливаемыми тепловой теоремой, служат след. равенства:
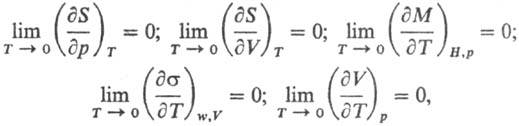
где S-энтропия, p и V-давление и объем фазы, М-общая намагниченность, H-напряженность магн. поля, s-поверхностное натяжение фазы на границе раздела с газовой (паровой) фазой, w-площадь пов-сти фазы. Т. обр., объем, намагниченность, поверхностное натяжение, др. термодинамич. св-ва вблизи абс. нуля т-ры перестают зависеть от т-ры. Тепловая теорема подразумевает, кроме того, что для теплоемкостей в-ва при постоянном давлении Ср и при постоянном объеме CV выполняется условие:
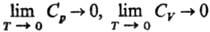
Важно, что эти утверждения м. б. получены теоретически, на основе положений квантовой теории твердого тела.
Тепловая теорема сформулирована для конденсир. фаз, однако это не является существ. ограничением ее применимости, т.к. при т-рах, близких к абс. нулю, все известные в природе в-ва находятся при конечном давлении в конденсир. состоянии.
Из тепловой теоремы следует утверждение о принципиальной недостижимости абс. нуля т-ры в к.-л. реальном процессе перехода с конечным числом операций. Существ. сложность представляют собой т.наз. замороженные фазы-стекла, нек-рые мол. кристаллы (СО, NO, N2O и др.). Это неравновесное состояние в-ва, сохраняющее ниже т-ры плавления структуру, присущую расплавам. Энтропия замороженной фазы больше энтропии равновесной фазы того же состава при той же т-ре, причем разница энтропии сохраняется вплоть до абс. нуля т-ры. Однако поскольку переход равновесная фаза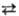 
замороженная фаза не относится к превращениям, происходящим между равновесными фазами, противоречия с тепловой теоремой не возникает. Утверждение о невозможности достижения абс. нуля т-ры с помощью процессов, в к-рые вовлечены замороженные фазы, справедливо.
Альтернативная формулировка тепловой теоремы предложена М. Планком (1911). Согласно этой формулировке, при абс. нуле т-ры энтропия любой равновесной конденсир. фазы равна нулю при любых значениях параметров состояния, т.е.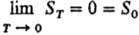 
. Формулировка Планка позволяет производить расчеты абс. энтропии в-в в любом агрегатном состоянии. Так, для 1 моля газа А абс. энтропия при т-ре T1 и давлении p определяется по ф-ле:
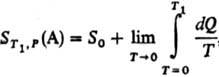
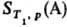
где S0 = 0-энтропия конденсир. в-ва А при абс. нуле т-ры,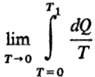 
-теплота, подведенная к системе для нагревания до т-ры T1 и перевода в-ва А в газ, к-рая м.б. измерена калориметрически.
Абс. энтропии приводятся в справочниках термодинамич. величин (см. Энтропия). Знание абс. энтропии помогает рассчитывать условия хим. равновесия (т. наз. метод абс. энтропии; см. Константа равновесия).
Формулировка Планка м.б. проверена путем сравнения результатов калориметрич. измерений и статистич. расчетов энтропии для газов. Для исследованных к настоящему времени в-в показано, что
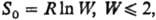
где R-газовая постоянная, W-термодинамич. вероятность, равная числу микросостояний системы, реализующих данное макросостояние (см. Статистическая термодинамика).
Лит. см. при статьях Термодинамические потенциалы, Химическая термодинамика. М. В. Коробов.