Диффузиoнно-контролируемые реакции
ДИФФУЗИOННО-КОНТРОЛИРУЕМЫЕ
РЕАКЦИИ, р-ции, скорость к-рых определяется
диффузионным сближением реагирующих частиц, после чего их взаимод. происходит
практически мгновенно. К диффузионно-контролируемым реакциям относятся: бимолекулярная рекомбинация атомов
и ионов в р-рах, рекомбинация и диспропорционирование радикалов и ион-радикалов,
р-ции молекул со своб. атомами или радикалами в твердом теле и др. Кинетика
диффузионно-контролируемых реакций описывается теорией, основанной на предположении о применимости к поступат.
самодиффузии молекул макроскопич. законов диффузии Фика; о влиянии диффузионного
массопереноса на кинетику хим. р-ций см. в ст. Макрокинетика. Теорию
диффузионно-контролируемых реакций применяют для объяснения мн. процессов, связанных с диффузией микрочастиц:
роста коллоидных частиц, электроосаждения, тушения люминесценции, диффузионного
горения (роль диффундирующих частиц играет окислитель, распространяющийся в
среде - капле горючего) и др. Кинетич. особенности
диффузионно-контролируемых реакций наглядно иллюстрируются на примере бимолекулярных процессов типа:
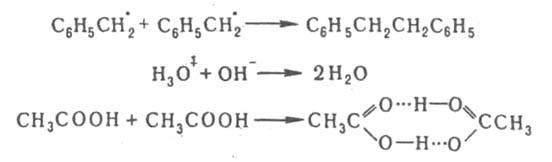
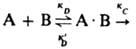продукты, где кD и к'D - константы скорости
образования и распада диффузионной пары соотв., а кС характеризует скорость превращения диффузионной пары в продукты р-ции. Наблюдаемая на опыте константа скорости р-ции кнабл = кCкD(к'D + кС)-1. При выполнении условия к'D >> кС бимолекулярная р-ция протекает в кинетич. режиме
и кнабл = кC = KАВ, где КАВ = кD/к'D ; при кC > кD процесс лимитируется диффузией и кнабл = кD .
Впервые проблема описания диффузионно-контролируемых реакций была проанализирована М. Смолуховским в применении к коагуляции коллоидов. В квазистационарном режиме скорость встречи частиц А и В: v = 4.10-3pDrNA[A][B] молъ/(л.с), где D -сумма коэф. диффузии частиц А и В (см2/с), r - сумма их радиусов (см), NA - постоянная Авогадро. Частицы при этом рассматриваются как сферы, а жидкость, в к-рой они диффундируют, - как изотропная среда. Квазистационарный режим р-ции устанавливается за время t ~ r2/D (в низковязких жидкостях t ~ 10-8 — 10-10 с). Если между частицами действуют силы притяжения или отталкивания (ионы или молекулы, обладающие дипольным моментом), то вместо R используют т. наз. эффективный радиус встречи (Reff):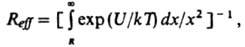
где U - потенциал межмолекулярных взаимодействий, k - постоянная Больцмана, Т - абс. т-ра. Коэф. диффузии связан с вязкостью р-рителя h. Согласно закону Стокса - Эйнштейна, для сферич. частицы радиуса r в изотропной среде D = 106kT/6prh и для двух одинаковых частиц кD = 2,7.103NAkT/h (л/моль.с). Опытные данные обычно подтверждают предсказываемую этим соотношением зависимость кD от Т/h, однако по абс. величине опытные и расчетные значения кD не всегда совпадают. Для лучшего совпадения вводят т. наз. фактор микротрения f, к-рый зависит от размеров диффундирующих частиц и молекул р-рителя, и используют ф-лу Стокса - Эйнштейна в виде: D= 10-6kT/6prhf. Описанная теория позволяет рассчитывать константы скорости рекомбинации радикалов, напр., нек-рых алкильных, алкоксильных и феноксилъных радикалов в углеводородных р-рителях, в хорошем согласии с экспериментом. В случае взаимод. частиц большого размера с определенным реакционным центром (атомом или атомной группой) на скорость диффузионно-контролируемых реакций существенно влияет взаимная ориентация частиц в структурной ячейке. Благоприятная для р-ции ориентация частиц, так же как и их встреча, обусловлена взаимными поворотами при случайных неупорядоченных столкновениях и потому рассматривается как результат вращат. и поступат. диффузии. Для р-ции многоатомных частиц требуется, как правило, их определенная взаимная ориентация. В этом случае реагенты обладают хим. анизотропией, к-рая характеризуется стерич. фактором Р [ 1. Диффузионно-контролируемые реакции химически анизотропных реагентов рассматривают как контролируемую диффузией встречу двух частиц - сфер с "черными пятнами", при к-рой происходит контакт черных пятен. Константа скорости такой р-ции кD = 4p10-3DNAReff л/(моль.с), где Reff связан с суммой радиусов частиц r и стерич. фактором Р соотношением:
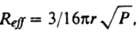т. е. кD прямо пропорциональна не Р, как для р-ций в газовой фазе, а
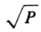вследствие повторных встреч частиц в клетке, к-рые
сопровождаются поворотом частиц, что приводит к усреднению Р.
Диффузионно-контролируемые реакции изучаются методами, разработанными для быстрых р-ций, в частности импульсным фотолизом, импульсным радиолизом, методом прерывистого освещения, ЭПР и др. Константы скорости рекомбинации атомов и радикалов в р-рах имеют значения порядка 109-108 л/(моль.с).
===
Исп. литература: Энтелис С. Г., Тигер Р. П., Кинетика реакций в жидкой фазе, М., 1973; Мелвин-Хьюз Э. А., Равновесие и кинетика реакций в растворах, пер. с англ., М., 1975; Овчинников А. А., Тимашев С. Ф., Белый А. А., Кинетика диффузионно-контролируемых химических процессов, М.. 1986. Е. Т. Денисов.