4.1.Интегральные и декомпозиционные методы расчета ХТС.
Суть интегральных методов расчета ХТС заключается в объединении систем уравнений, описывающих работу отдельных аппаратов, в одну большую систему уравнений с дальнейшим решением этой системы. При декомпозиционном методе расчета ХТС представляется в виде отдельных блоков, соответствующих элементам ХТС, и, расчет ХТС сводится к последовательному расчету отдельных блоков. В данном случае размерность каждой отдельной системы уравнений, соответствующей блоку ХТС, относительно невелика. Сравним характеристики интегрального и декомпозиционного методов расчета ХТС:
Как было указано выше, суть интегрального метода заключается в объединении систем уравнений, описывающих работу отдельных аппаратов, в одну большую систему уравнений с дальнейшим решением этой системы. Таким образом, линейные уравнения материального и теплового балансов объединяются с нелинейными уравнениями равновесия химических реакций, дифференциальными линейными и нелинейными уравнениями, уравнениями гидродинамики в частных производных и т.д. в единую "большую" систему уравнений, например, в общем виде:

Данная система уравнений содержит множество уравнений различного типа от линейных до дифференциальных уравнений в частных производных. Такие системы уравнений называются смешанными и требуют специальных математических методов для своего решения. Более того, в зависимости от типа уравнений (сложность которых определяется типом модулей), методы решения системы уравнений могут иметь чисто математические ограничения и требовать специального представления задачи. Это приведет к тому, что для конкретной ХТС должна составляется уникальная система уравнений. В связи со сложностью, система уравнений может быть трудноразрешима, и требовать применения специальных математических методов. Следовательно, перед использованием интегрального метода необходимо с математической точки зрения предварительно проанализировать математические зависимости, лежащие в основе модулей ХТС.
Таким образом, для использования интегрального метода проектировщику необходимо иметь достаточно серьезную математическую подготовку и специальные компьютерные программы для решения смешанных систем уравнений (линейных, нелинейных, дифференциальных, в частных производных и др.). Однако даже в этом случае, с целью оперативного получения результатов расчета, интегральный способ расчета можно рекомендовать только для простых ХТС или для ХТС, где необходимо рассчитать только материальные балансы без учета кинетики, термодинамики и т.д. (т.е. решить линейную систему уравнений).
Суть декомпозиционного метода расчета заключается в том, что ХТС представляется в виде отдельных блоков, соответствующих элементам ХТС. Расчет ХТС сводится к последовательному расчету отдельных блоков. В этом случае, при расчете отдельного модуля требуется рассчитать только ограниченное количество уравнений, соответствующих конкретному модулю, т.е. выполнить проверочный расчет конкретного процесса. Следует отметить, что при наличии ограниченного количества возможных модулей ХТС, их алгоритмы расчета давно разработаны и приведены в специальной литературе и в виде компьютерных программ (данные алгоритмы также преподавались в курсе "Моделирование ХТП"). Именно поэтому, вследствие своей универсальности, наибольшее распространение, как при расчете сложных, так и простых ХТС, получил декомпозиционный способ расчета.
Как известно, большинство ХТС имеет рециркуляционные соединения, образующие замкнутую ХТС, непосредственный расчет которой с помощью декомпомпозиционного принципа невозможен. Для решения таких систем их структуру сначала необходимо привести к разомкнутому виду, и, только затем производить расчет с использованием декомпозиционногоспособа расчета. Однако, не смотря на то, что теория и алгоритмы анализа структуры ХТС с целью определения оптимального множества разрываемых связей с целью перевода структуры из замкнутого к разомкнутому виду, и нахождения оптимальной последовательности расчета ХТС, достаточно хорошо разработаны, каждая ХТС сама по себе уникальна. В связи с этим, в конкретном случае могут возникнуть проблемы нахождения оптимального множества разрываемых связей и оптимальной последовательности расчета декомпозиционным способом.
Существуют разновидности декомпозиционного способа расчета замкнутых ХТС, наиболее простым из которых является итерационный способ расчета. Рассмотрим итерационный способ расчета замкнутых ХТС на примере простейшей схемы, представленной на Рис.4.1.
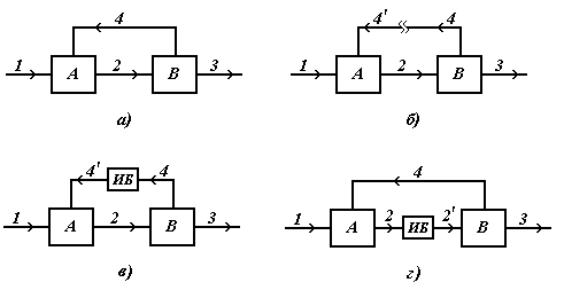
Рис.4.1. Иллюстрация итерационного способа расчета ХТС
Как видно на Рис.4.1а, простейшая замкнутая ХТС состоит из двух модулей (А и В), связанных четырьмя технологическими связями, из которых связь 4 является рециркуляционной. Исходя из исходной задачи расчета ХТС, исходными данными для расчета указанной ХТС будут параметры функционирования элементов А и В, а также параметры входящего в ХТС потока номер 1. Однако, провести расчет модуля А с целью получения параметров потока 2 невозможно, т.к. неизвестны параметры потока 4. Расчет модуля В произвести также невозможно, т.к. неизвестен поток 2, входящий в этот модуль. Таким образом, непосредственное применение декомпозиционного способа расчета этой замкнутой ХТС невозможно.
Для того чтобы декомпозиционный способ можно было применить, необходимо привести ХТС из замкнутого вида к разомкнутому. Для этого, в случае указанной ХТС, можно "разорвать" любой поток, входящий в рецикл, т.е. поток 2 или 4. В случае разрыва потока 4 (см.Рис.4.1б), выходящего из модуля В и входящего в модуль А, образуется новый входящий в ХТС и в модуль А поток 4'. В связи с тем, что деление потока на 4 и 4' является условным (применяемым только для цели перевода структуры ХТС из замкнутого к разомкнутому виду), то при применении итерационного способа расчета, в место разрыва помещается дополнительный модуль – итерационный блок (ИБ) (см.Рис.4.1в). В этом случае, исходя из исходной задачи расчета ХТС, исходными данными для расчета указанной ХТС будут являться параметры функционирования элементов А и В, а также параметры входящих потоков 1 и 4'. Первоначальные параметры потока 4' могут определяться с применением какого-либо алгоритма расчета и на основании заданных исходных данных.
С указанным набором исходных данных появляется возможность выполнить ПЕРВЫЙ расчет ХТС, т.е. определить параметры потока 2, зная которые рассчитать параметры потоков 3 и 4. В данном случае, параметры потока 4 будут отличаться от параметров потока 4', поэтому, итерационный блок, проанализировав оба набора данных (потоков 4 и 4'), рассчитает суммарную погрешность и присвоит новые значения параметров потока 4'. Так как новые значения потока 4' будут формироваться итерационным блоком с учетом расчетных параметров потока 4, то при выполнении ВТОРОГО расчета ХТС, суммарная погрешность будет меньше, чем при первом расчете. Далее, циклические расчеты (итерации) проводятся до тех пор, пока значения суммарной погрешности не будут ниже требуемой точности расчета.
Итерационный метод расчета ХТС обычно применяется для расчета относительно простых ХТС, т.к. применение данного метода для сложных ХТС является не достаточно эффективным, т.к. предусматривает последовательные приближения искомых параметров потоков. В связи с тем, что элементы ХТС, исходя из их физико-химической природы, могут функционировать лишь в заданных интервалах изменения параметров, применение итерационного метода иногда может быть невозможно, т.к. в процессе сходимости этого математического метода, значения технологических параметров могут выйти за пределы функционирования элементов ХТС. При расчете ХТС, имеющей несколько разрываемых потоков (наличие нескольких рециклов), применение итерационного метода вообще может быть достаточно проблематично, т.к. вследствие наличия технологических связей, итерационные процессы будут взаимосвязаны, что негативно повлияет на достижение решения для всей системы.
При расчете сложных ХТС, имеющих несколько разрываемых потоков, обычно применяются методы многомерной минимизации суммарной погрешности, описанные в специальной литературе (например /9/). Суть этих методов заключается в том, что в отличие от итерационного метода, искомые значения параметров потоков рассчитываются при проведении расчета, с помощью специальных математических методов с ограничениями, наличие которых не позволяет выйти за пределы функционирования технологических операторов (в процессе нахождения решения), что позволяет достичь сходимости намного быстрее и надежнее.
Как было указано выше, рецикл можно привести из замкнутого вида к разомкнутому виду путем разрыва одной из технологических связей, входящих в рецикл. На Рис.4.1г представлен вариант разрыва потока 2. В этом случае, имея начальные приближения параметров потока 2', сначала будет рассчитываться модуль В с определением параметров потоков 3 и 4, а затем модуль А с определением параметров потока 2. В отличие от предыдущего варианта, итерации будут проводиться по параметрам потока 2, а не потока 4. Вопросы выбора оптимальных вариантов перевода ХТС из замкнутого к разомкнутому виду будут рассмотрены далее.
Сравнение особенностей интегрального и декомпозиционного методов расчета ХТС представлены в Таблице 4.1.
Таблица 4.1.
Сравнительные характеристики интегрального и
декомпозиционного методов расчета ХТС.
| Интегральный метод | Декомпозиционный метод |
Способ представления задачи | |
Глобальная система уравнений | Отдельные моделирующие блоки, стыкующиеся с помощью координирующей программы |
Способ решения задачи | |
Совместное решение уравнений | Последовательный расчет с использованием итерационного метода расчета, и, с предварительным анализом ХТС для выявления оптимальной последовательности расчета ХТС. |
Достоинства | |
Возможность проведения расчета для любого набора неизвестных переменных | Меньшее количество вычислений, наглядность |
Недостатки | |
Большая размерность единой системы уравнений наряду с отсутствием надежных методов решения смешанных систем линейных, нелинейных и дифференциальных уравнений большой размерности. Уникальность каждой системы уравнений. | Трудность построения оптимального алгоритма расчета ХТС. |
Рекомендации | |
Применять только при расчетах упрощенных ХТС | Применять для расчета ХТС произвольной сложности. |