4.2.2. Определение оптимальной последовательности расчета ХТС.
Задача определения оптимальной последовательности расчета ХТС завершает анализ структуры ХТС и выполняется в два этапа. На первом этапе производят анализ структуры ХТС в целом с выделением комплексов ХТС и определением предварительного порядка расчета ХТС, а также определяют все контуры, входящие в выделенные комплексы. На втором этапе производят анализ структуры комплексов, определяют связи, разрыв которых позволяет перевести комплексы к разомкнутому виду, и определяют окончательную последовательность расчета ХТС.
Существует множество различных алгоритмов выделения комплексов, которые связаны с вариантом формализации ХТС. Обычно, данные алгоритмы связаны с матричными операциями, и с дальнейшим преобразованием получившихся матриц с помощью логических операций. Данные методы достаточно хорошо разработаны и подробно представлены в литературе. В связи с тем, что специалист, проводящий анализ структуры ХТС обычно автоматически использует уже готовые разработки, в настоящем конспекте лекций данные методы не приводятся.
В отличие от методов выделения комплексов, алгоритмы поиска оптимального множества разрываемых связей комплекса, не имеют однозначного решения, т.к. сама структура графа не содержит информацию об особенностях его связей.
Понятие параметричности связи (потока), т.е. количества параметров, характеризующим поток в конкретном рассмотрении, является обобщающим, и связано как со свойствами потока, так и с алгоритмом расчета модулей, откуда интересующая связь выходит и куда направлена. При поиске оптимального множества разрываемых связей необходимо учитывать правило: суммарная параметричность разрываемых связей комплекса должна быть минимальна. Рассмотрим понятие параметричности на примере.
В качестве примера рассмотрим схему движения материальных потоков в радиантной части котла с естественной циркуляцией (Рис.4.7).
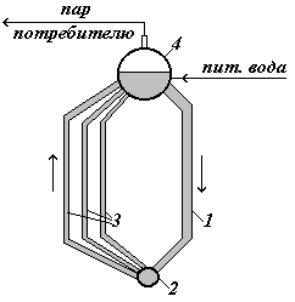
Рис.4.7. Принципиальная технологическая схема котла
В соответствии с технологической схемой, питательная вода из барабана котла (4) по опускным трубам (1) подается в коллектор (2), а затем распределяется по испарительным трубам (3). Образовавшаяся в испарительных трубах паровая фаза за счет разности плотностей поднимается вместе с жидкостью вверх, в барабан. В барабане котла сухой насыщенный пар сепарируется от жидкости и подается потребителю. Расход пара компенсируется подачей питательной воды таким образом, чтобы уровень в барабане котла оставался постоянным. Операторная схема и граф указанной технологической схемы представлены на Рис.4.8.
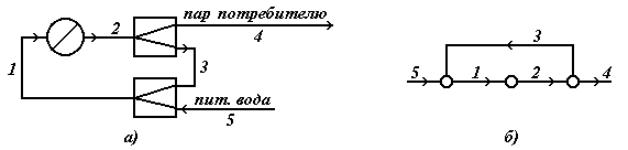
Рис.4.8. Операторная схема (а) и граф схемы (б) котла
Граф, представленный на рисунке имеет один комплекс, включающий потоки 1, 2 и 3, входящие в один контур. Перед тем, как определить количество параметров, которыми можно охарактеризовать состояние потоков, входящих в комплекс, рассмотрим фазовое состояние потоков: 1 – Жидкость, 2 – Пар+Жидкость, 3 – Жидкость. Для того, чтобы охарактеризовать состояние жидких потоков (1 и 3), состоящих из воды, необходимо знать их: общий расход и температуру. Для того, чтобы охарактеризовать параметры парожидкостного потока (2), необходимо знать: общий расход, температуру и долю паровой фазы (степень сухости). Кроме того, так как в системе есть барабан, т.е. модуль, где достигается парожидкостное равновесие, то необходимо знать давление каждого потока. Однако можно допустить, что в котле (т.е. для всех потоков) происходит изобарный процесс, поэтому давление из параметров потоков можно исключить.
Таким образом, параметричность потоков (количество характеризующих в данном рассмотрении параметров) будет следующая:
| Поток | Параметричность |
| 1 | 2 |
| 2 | 3 |
| 3 | 2 |
В соответствии с правилом выбора разрываемых потоков "суммарная параметричность разрываемых связей комплекса должна быть минимальна" можно заключить, что для перевода комплекса из замкнутого в разомкнутое состояние, можно разорвать поток 1 или 3.
При разрыве потока 1, входными в данную ХТС потоками будут потоки: 5 и 1', а выходными: 4 и 1, причем, при достижении решения, расход и температура потоков 1 и 1' должны быть одинаковые. Для обеспечения возможности расчета ХТС, в место разрыва будет установлен итерационный блок ИБ (см.Рис.4.9), основными задачами которого будут: определение суммарной погрешности по изменяющимся в процессе расчета параметрам (расходу и температуре) потоков 1 и 1', и определение параметров потока 1' при известных параметрах потока 1 в соответствии с выбранным математическим методом сходимости.
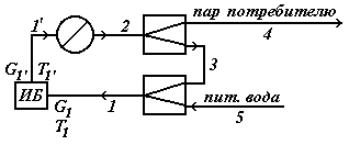
Рис.4.9. Операторная схема с итерационным блоком
Так как параметричность характеризует количество параметров, которые могут изменяться, то решение ХТС декомпозиционным методом будет происходить до тех пор, пока величина суммарной погрешности (Err), с учетом заданных весовых коэффициентов (wG, wTи т.д.), не будет меньше или равна заданной точности расчета (Eps):
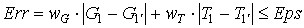 [4.1]
[4.1]
Величины весовых коэффициентов обычно выбираются таким образом, чтобы уравнять вклад различных по абсолютной величине значений параметров в ошибку.
Следует отметить, что в случае разрыва потока 2, имеющего большую параметричность, точность расчета комплекса необходимо будет рассчитывать не по двум параметрам (G и T), а по трем (G, T и X), что значительно сложнее и потребует больших затрат на достижение решения. Кроме того, необходимо учесть, что всегда существуют математические проблемы сходимости расчета систем вне зависимости от способа их расчета.
При расчете более сложных ХТС достаточно часто встречаются случаи, когда комплекс имеет более одного контура, и один из потоков является общим (см.Рис.4.10).
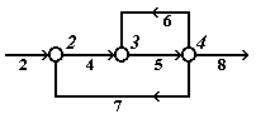
Рис.4.10. Иллюстрация комплекса, имеющего два контура
Для разрыва контура 2-3-4-2 (по вершинам), в зависимости от параметричности потоков, можно разорвать любой из потоков: 4, 5 или 7. Для разрыва контура 3-4-3 (по вершинам), в зависимости от параметричности потоков, можно разорвать поток 5 или 6. Таким образом, поток 5 является общим, следовательно, при его разрыве одновременно будут разорваны оба контура. При этом можно утверждать, что параметричность одного потока всегда будет меньше суммарной параметричности двух потоков, которые необходимо было бы разорвать при разрыве двух контуров. В случае более сложной структуры комплекса (три и более контуров комплекса имеют один общий поток), последнее утверждение уже не будет вызывать сомнений.
Таким образом, можно сформулировать следующие правила перевода комплекса из замкнутого вида к разомкнутому (разрыва потоков):
1. В комплексе всегда разрывается множество потоков, имеющих наименьшую суммарную параметричность;
2. Если в комплексе имеются потоки, одновременно входящие в несколько контуров комплекса, то эти потоки могут быть разорваны без дополнительного анализа величины их параметричности.
После определения оптимального множества разрываемых контуров, суммарная параметричность которых минимальна, появляется возможность определить окончательную последовательность расчета всей ХТС с учетом разрываемых потоков, т.е. с учетом выходящих из итерационных блоков потоков, которые для ХТС переведенной из замкнутого к разомкнутому виду также будут входными. Далее, окончательная последовательность расчета ХТС передается в координирующее программное обеспечение, которое позволяет составить из модулей базы данных составить ХТС заданного вида и произвести ее расчет.