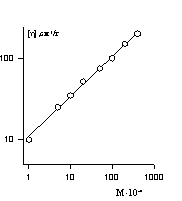5.2.2. Методы определения молекулярной массы полимеров по свойствам растворов
Свойства растворов
Наиболее часто среднечисленную молекулярную массу 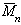 полимеров находят методом осмотического давления, который основан на изучении явления осмоса - одностороннего проникновения молекул растворителя через полупроницаемую мембрану, не пропускающую молекулы полимера. Количественной характеристикой явления осмоса служит осмотическое давление, пропорциональное числу молекул в единице объёма раствора.
полимеров находят методом осмотического давления, который основан на изучении явления осмоса - одностороннего проникновения молекул растворителя через полупроницаемую мембрану, не пропускающую молекулы полимера. Количественной характеристикой явления осмоса служит осмотическое давление, пропорциональное числу молекул в единице объёма раствора.
Молекулярная масса определяется как коэффициент, связывающий весовую и частичную концентрации
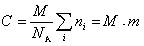 , (2.5.12)
, (2.5.12)
где С – весовая концентрация, г/см3; 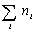 - суммарная частичная концентрация, молекул/см3;
- суммарная частичная концентрация, молекул/см3;  - мольная концентрация, моль/см3.
- мольная концентрация, моль/см3.
Таким образом, задача сводится к определению мольной концентрации раствора известной весовой концентрации.
Стремление молекул растворителя к самопроизвольному проникновению через мембрану определяется разностью химических потенциалов растворителя в частях системы, разделенных перегородкой, причем 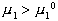 , так как из химической термодинамики известно, что для растворов
, так как из химической термодинамики известно, что для растворов
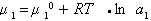 ,
,
где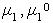 - химический потенциал раствора при активности раствора aи стандартный химический потенциал.
- химический потенциал раствора при активности раствора aи стандартный химический потенциал.
Осмотическое давление раствора
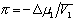 , (2.5.13)
, (2.5.13)
где 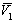 – парциальный мольный объём растворителя, p - служит количественной мерой сродства между компонентами раствора.
– парциальный мольный объём растворителя, p - служит количественной мерой сродства между компонентами раствора.
Связь между осмотическим давлением и весовой концентрацией растворов описывается следующими уравнениями:
(уравнение Вант-Гоффа) для растворов низкомолекулярных веществ
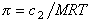 , (2.5.14)
, (2.5.14)
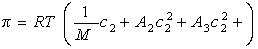
или
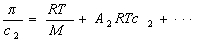 , (2.5.15)
, (2.5.15)
где А2 – второй вириальный коэффициент, характеризующий взаимодействие полимера с растворителем и форму макромолекул в растворе, обычно А3®0.
Рис. 2.50. Зависимость приведенного осмотического давления от концентрации раствора полиизобутилена в циклогексане. |
Величина p /c2 носит название приведенного осмотического давления. На рис. 2.50 показан пример зависимости приведенного осмотического давления для растворов полимера в различных растворителях. Чем больше наклон прямых, тем сильнее проявляется взаимодействие между компонентами раствора и тем больше величина
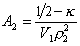 , (2.5.16)
, (2.5.16)
где k- параметр взаимодействия, r2 – плотность полимера в растворе, V1 – мольный объём растворителя.
При k = 0,5 А2 =0 и раствор ведет себя как идеальный. Таким образом, определяя наклон зависимости p /c2 = fc2 , можно охарактеризовать сродство компонентов раствора. Величина молекулярной массы определяется как
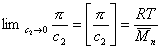 . (2.5.17)
. (2.5.17)
Найденная из измерений осмотического давления молекулярная масса характеризует 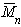 .
.
Метод светорассеяния. Среднемассовая молекулярная масса 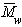
Явление светорассеяния в растворах полимеров наблюдается в том случае, если размер макромолекул менее l/2 - половины длины волны проходящего света. Существуют различные теории рассеяния света, положенные в основу расчетных уравнений экспериментальных методов определения молекулярной массы. При условии, что размер молекул полимера меньше l/2, для растворов полимеров справедлива теория рассеяния света Эйнштейна.
Если рассеяние света происходит на сферических частицах, то интенсивность рассеяния будет одинаковой во всех направлениях. Обозначим угол, под которым по отношению к падающему лучу определяется интенсивность рассеянного света, Q. Рассеивающая способность характеризуется коэффициентом рассеяния R:
 (2.5.18)
(2.5.18)
где IQ, I0- интенсивность рассеянного и падающего света; l– расстояние, на котором наблюдается рассеянный свет от рассеивающего объёма; v – рассеивающий объём.
В практике определения интенсивности рассеянного света наиболее часто определяется R90, т.е. рассеяние света под углом 90o, хотя с помощью современных приборов, особенно использующих в качестве источника света лазер, можно определять интенсивность рассеянного света от Q = 4o.
Для расчета молекулярной массы полимеров используется уравнение Дебая:
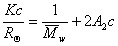 , (2.5.19)
, (2.5.19)
где с – весовая концентрация, г/см3; K – оптическая постоянная, зависящая от коэффициента преломления среды (n0), концентрационного инкремента коэффициента преломления раствора (dn/dc) и длины волны света l,
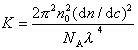 . (2.5.20)
. (2.5.20)
Таким образом для определения молекулярной массы следует измерять угловое рассеяние света, коэффициент преломления среды. Особенно тщательно следует определять (dn/dc), так как эта величина обычно чрезвычайно мала. Следует привлекать приборы, позволяющие определить коэффициент преломления с точностью до 6-го знака.
По аналогии с поглощением света можем записать для интенсивности рассеяния
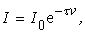 (2.5.21)
(2.5.21)
гдеt – мутность 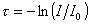 при v =1; I – интенсивность света, прошедшего через раствор после рассеяния.
при v =1; I – интенсивность света, прошедшего через раствор после рассеяния.
Мутность связана с коэффициентом рассеяния соотношением
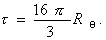 (2.5.22)
(2.5.22)
Поэтому, с учетом уравнения (2.5.19), можно проводить расчет молекулярной массы по уравнению
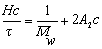 , (2.5.23)
, (2.5.23)
где Н – оптическая постоянная, Н = 16p K/3.
Для расчета молекулярной массы определяется величина
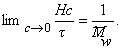
По углу наклона можно определить значение А2 и охарактеризовать взаимодействие компонентов раствора. Изменение температуры, замена растворителя могут вызвать изменение межмолекулярного взаимодействия компонентов раствора и формы макромолекул в растворе.
Молекулы могут приобретать и асимметрическую форму. В этом случае рассеяние света под разными углами к падающему лучу будет неравномерным и найденное значение молекулярной массы содержит погрешность. Поэтому необходимо вводить поправку на внутреннюю интерференцию света, появляющуюся в результате рассеяния света с некоторой разностью фаз от различных участков молекул. Для введения поправок существуют два основных метода: метод Дебая и метод Зимма.
Метод Дебая основан на измерении интенсивности рассеянного света при значении углов рассеяния, равных 135 и 45o, соответственно R45 и R135. Отношение интенсивности равно отношению поправок Р и называется коэффициентом асимметрии
z = R 45 /R135 = P45 / P135 . (2.5.24)
Величина z зависит от концентрации раствора, так как форма макромолекул в растворе может изменяться с увеличением концентрации. Для определения истинного значения z строят зависимость 1/(z-1)=fс и определяют 1/([z]-1) = limс®0 1/(z-1).
Зная z,по существующим таблицам находят величину Р, которую вводят в расчетное уравнение
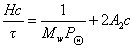 . (2.5.25)
. (2.5.25)
Метод Зимма основан на построении специальной диаграммы, на которой по оси абсцисс откладывается и концентрация, и угол рассеяния света. Линии на диаграмме образуют два семейства параллельных (практически прямых) линий. Более крутые линии представляют собой зависимость рассеяния света от концентрации растворов. Более пологие – зависимость рассеяния света от угла определения. Нижняя линия соответствует рассеянию света при с = 0, крайняя левая - дает совокупность точек при sin Q/2 =0. Обе прямые пересекаются с осью ординат в точке, характеризующей 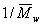 . Этот метод более точный, чем метод Дебая и позволяет рассчитать молекулярную массу полимера, не определяя и не постулируя форму макромолекул в растворе.
. Этот метод более точный, чем метод Дебая и позволяет рассчитать молекулярную массу полимера, не определяя и не постулируя форму макромолекул в растворе.
Комбинированный метод измерения диффузии и вязкости
Для определения молекулярной массы полимеров можно измерять коэффициент диффузии растворенного вещества. Если представить, что макромолекулы имеют узкое распределение по молекулярной массе и каждая молекула не взаимодействует с другими молекулами полимера, то для молекулы, перемещающейся вдали от стенки сосуда, сила трения со средой может быть описана выражением
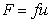 , (2.5.26)
, (2.5.26)
где F- сила трения; u – скорость перемещения молекулы; f =6ph0r- коэффициент трения сферических частиц; h0 – вязкость растворителя; r – радиус макромолекулы в растворе.
Уравнение (2.5.26) справедливо при скорости перемещения макромолекул 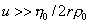 , гдеr0 – плотность растворителя.
, гдеr0 – плотность растворителя.
Предполагая применимость уравнения Эйнштейна для диффузии полимерных молекул в растворе, запишем
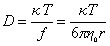 . (2.5.27)
. (2.5.27)
Молекулярная масса сферических макромолекул определяется как масса 1 моля полимера:
 . (2.5.28)
. (2.5.28)
Сочетание (2.5.27) и (2.5.28) дает
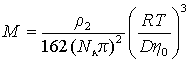 . (2.5.29)
. (2.5.29)
Cущественную ошибку может внести в расчет использование в качестве r2 значения плотности полимера, так как в растворе плотность макромолекул может значительно отличаться от плотности “сухого” полимера. Поэтому следует использовать значение 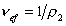 , которое можно определить из измерений вязкости.
, которое можно определить из измерений вязкости.
Тогда
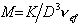 , (2.5.30)
, (2.5.30)
где vef- это тот удельный объём, который занимают макромолекулы в растворе, см3/г, учитывающий взаимодействие макромолекул в растворителе.
Вискозиметрический метод определенияvef и 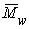 .
.
Существуют несколько уравнений, связывающих вязкость растворов полимеров с их концентрацией. Уравнение Симха для сферических частиц связывает удельную вязкость с объёмной концентрацией полимера:
 , (2.5.31)
, (2.5.31)
где j – объёмная доля, занимаемая полимером, 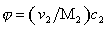 ; c2- массовая концентрация (г/см3); vef- эффективный объём одного моля полимера.
; c2- массовая концентрация (г/см3); vef- эффективный объём одного моля полимера.
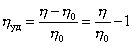 ,
,
где h0 – вязкость растворителя; h – вязкость раствора; (h/h0) – относительная вязкость.
Поэтому
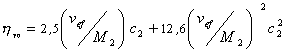 . (2.5.32)
. (2.5.32)
В общем виде
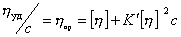 , (2.5.33)
, (2.5.33)
где  – характеристическая вязкость, a- коэффициент Эйнштейна формы макромолекул в растворе.
– характеристическая вязкость, a- коэффициент Эйнштейна формы макромолекул в растворе.
Уравнение (2.5.33) носит название уравнения Хаггинса, K' – постоянная Хаггинса, характеризующая форму макромолекул в растворе. Для сферических макромолекул K' = 2, для эллипсоид-
ных K' = 2¸10; для игольчатых форм K'<2 и может быть даже отрицательной.
|
Рис. 2.52. Зависимость характеристической вязкости от молекулярной массы полиизобутилена в бензоле |
Для определения vef строится зависимость hпр от концентрации раствора (рис. 2.51.). Из значения [h] находится величина vef, которая затем подставляется в уравнение (2.5.30).
Расчет молекулярной массы из вискозиметрических данных (рис 2.52.) проводится по эмпирическому уравнению Марка-Хаувинка-Куна 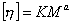 . Расчет молекулярной массы по этому уравнению можно проводить только в том случае, если постоянные K и а откалиброваны, для чего на ряде фракций данного полимера предварительно изучается зависимость [h] от молекулярной массы.
. Расчет молекулярной массы по этому уравнению можно проводить только в том случае, если постоянные K и а откалиброваны, для чего на ряде фракций данного полимера предварительно изучается зависимость [h] от молекулярной массы.
Для этого уравнение приводят к линейному виду
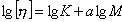 . (2.5.34)
. (2.5.34)
По этой зависимости определяют постоянные а и K. Для многих полимеров эти постоянные приведены в таблицах. Следует помнить, что постоянные приводятся при заданной температуре и для определения молекулярной массы следует использовать тот же растворитель, для которого найдены эти постоянные. Если в процессе синтеза могут образовываться разветвленные молекулы, то степень разветвления также сказывается на точности определения молекулярной массы полимеров этим методом, так как постоянные а и K зависят от формы макромолекул, а последняя изменяется при разветвлении. При калибровке постоянных уравнения Марка-Хаувинка-Куна следует определять характеристическую вязкость не менее чем пяти относительно однородных фракций полимера.
Определения молекулярной массы вискозиметрическим методом удобны и просты. Однако следует всегда помнить о возможных погрешностях на применимость этого метода.
Метод седиментации- один из наиболее точных методов определения молекулярной массы полимеров. Для анализов используется ультрацентрифуга, которую разработал шведский ученый Уве Сведберг в 1926 г. Он же предложил метод расчета молекулярной массы полимеров по скорости осаждения. За эти разработки он был удостоен Нобелевской премии.
Если предположить, что макромолекулы имеют узкое распределение по молекулярной массе (а в идеальном случае – монодисперсны), то сила, действующая на молекулу в центробежном поле,
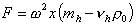 , (2.5.35)
, (2.5.35)
где F– сила, действующая на молекулу полимера; w2x – ускорение центробежного поля, w – угловая скорость вращения; x – расстояние от молекулы до центра вращения; mh – масса одной сольватированной молекулы; vh – объем одной молекулы, r0 - плотность растворителя, vhr0 – поправка на выталкивающую силу.
Масса одной сольватированной молекулы, в соответствии с концепцией сольватированной частицы Онслея, определяется как
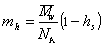 , (2.5.36)
, (2.5.36)
где hs- число сольватации макромолекул (г/г).
Объем одной сольватированной макромолекулы
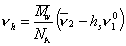 , (2.5.37)
, (2.5.37)
где v2- парциальный удельный объем макромолекул, см3/г; hsv10- поправка на объем связанного растворителя; v10 = 1/r0 – - удельный объем растворителя, см3/г.
С учетом (2.5.36) и (2.5.37) запишем уравнение (2.5.35) в виде
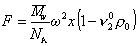 . (2.5.38)
. (2.5.38)
Можно видеть, что величина сольватации hs исключается из расчетного уравнения. Сила трения, уравновешивающая центробежную силу в стационарном режиме,
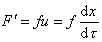 . (2.5.39)
. (2.5.39)
Из условия стационарности F= F', следовательно,
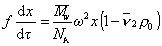 . (2.5.40)
. (2.5.40)
Для перехода от дифференциальной формы уравнения к интегральной Сведберг предложил использовать понятие постоянной седиментации
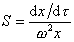 , (2.5.41)
, (2.5.41)
характеризующей скорость осаждения макромолекул под действием единицы центробежного поля. Эта постоянная зависит только от свойств макромолекул.
Коэффициент трения может быть определен из измерения коэффициента диффузии по уравнению Эйнштейна
 ,
,
поэтому
 . (2.5.42)
. (2.5.42)
Уравнение (2.5.42) носит название уравнения Сведберга. Коэффициент диффузии D и коэффициент седиментации s определяются независимо. Для исключения эффекта взаимодействия макромолекул значение s экстраполируют к бесконечно малой концентрации и в расчетах используют значение s0.
Метод седиментации позволяет наиболее точно определить значение молекулярной массы полимера, так как здесь не надо определять или предполагать форму макромолекул, а величина сольватации исключается из расчетного уравнения. Экспериментально установлено, что
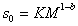 . (2.5.43)
. (2.5.43)
гдеK и b – постоянные, для многих полимеров приведенные в таблицах. Поэтому после калибровки постоянных уравнение (2.5.43) можно использовать для определения молекулярной массы без привлечения диффузионных измерений.
Определение средней молекулярной массы методом
диффузионно-седиментационного равновесия.
По этому методу не проводят осаждения полимера, а ведут процесс только до установления равновесия между седиментацией и диффузией.
Для седиментационного потока
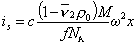 . (2.5.44)
. (2.5.44)
Для диффузионного потока
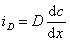 . (2.5.45)
. (2.5.45)
При седиментационно-диффузионном равновесии iD= is, следовательно,
 . (2.5.46)
. (2.5.46)
После преобразования с учетом D = kT/f и kNА=R получаем
 . (2.5.47)
. (2.5.47)
Откуда после интегрирования
 . (2.5.48)
. (2.5.48)
Таким образом достаточно определить значения концентрации раствора в двух точках кюветы чтобы рассчитать значение Mz . Этот метод носит название метода Арчибальда. Можно проводить расчет и по неустановившемуся равновесию, что значительно сокращает время эксперимента, но усложняет расчет.
Кроме определения молекулярной массы метод седиментационного ультрацентрифугирования в сочетании с вискозиметрией позволяет охарактеризовать форму макромолекул в растворе, определяя фактор Шераги - Манделькерна b, который для сферических частиц равен b = 2,12×106.
Расчет проводится по формуле
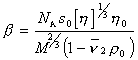 , (2.5.49)
, (2.5.49)
где s0 – коэффициент седиментации, экстраполированный к бесконечному разбавлению; [h] – характеристическая вязкость;h0 – вязкость растворителя.
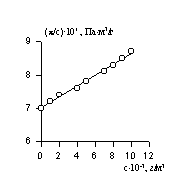
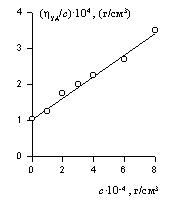 Рис.2.51. Зависимость приведенной
Рис.2.51. Зависимость приведенной