3.5.1. Теория быстрой коагуляции

Поскольку, как говорилось выше, при быстрой коагуляции любое столкновение оказывается эффективным, то разработка теории быстрой коагуляции оказалась более простой задачей и именно такая теория была разработана М. Смолуховским в 1916 г.

При разработке своей теории он исходил из следующих предпосылок:

1) частицы дисперсной фазы сферические, а сами дисперсные системы являются монодисперсными, т.е. содержат частички одного размера;

2) скорость коагуляции определяется тремя факторами:

– радиусом сферы сил притяжения частиц;

– интенсивностью броуновского движения, которая определяет число столкновений в единицу времени и характеризуется коэффициентом диффузии D;

– начальной концентрацией частиц n₀;

3) между частицами существуют только силы притяжения.

Последняя предпосылка означает, что в какой-то момент времени, который можно обозначить как t₀, внезапно и полностью исчезают силы, приводившие к отталкиванию частиц при их сближении. После этого времени любое столкновение частиц обязательно приведет к их агрегированию.

Смолуховский предложил рассматривать процесс коагуляции как попарное слипание частиц, чем формально уподобил процесс коагуляции химической реакции второго порядка. Считается, что вероятность одновременного столкновения трех частиц столь мала, что такие столкновения можно не учитывать.

Очевидно, что вначале будут образовываться агрегаты частиц, состоящие из двух первичных, затем первичная частица может объединяться с агрегатом из двух первичных частиц и образуется новый агрегат, состоящий из трех первичных частиц. Затем к нему присоединится еще одна частица и будет сформирован агрегат из четырех частиц и т.д. Назовем число частиц в агрегате порядком агрегата и будем считать, что при коагуляции последовательно будут сформированы агрегаты второго n₂, третьего n₃, четвертого n₄, пятого n₅ и т.д. порядков. В любой момент времени после начала коагуляции в дисперсной системе будет присутствовать набор агрегатов частиц, так что частичная концентрация будет определяться суммой всех агрегатов:

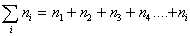. (2.3.137)

Выражая скорость коагуляции через уменьшение числа частиц в единице объема за единицу времени и учитывая, что общее число частиц может только уменьшаться, записываем

v = – dn/dt = kn², (2.3.138)

где v – скорость коагуляции, k – постоянная скорости коагуляции, n – частичная концентрация (частиц/м³).

Выяснение физического смысла постоянной скорости коагуляции проводится при рассмотрении диффузионного механизма сближения частиц.

Вначале решают задачу диффузионного сближения произвольной частицы с некоторой закрепленной в пространстве центральной частицей. Столкновение этой неподвижной частицы с другой происходит каждый раз, когда частицы сближаются на расстояние, равное их двойному радиусу(R = 2r). Таким образом, рассматривается диффузия точечных частиц к сфере радиуса R. При этом концентрация единичных (первичных) частиц на поверхности такой сферы равна нулю, поскольку на этой поверхности частицы образуют агрегаты.

Распределение частичной концентрации в дисперсной системе находят решением дифференциального уравнения диффузии (второго закона Фика)

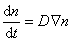, (2.3.139)

где 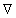– оператор Лапласа,

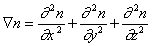. (2.3.140)

В операторе Лапласа x, y, z характеризуют координаты точечной частицы относительно центра сферы радиуса R. Считается, что в начальный момент распределение частиц в объеме дисперсной системы можно принять равномерным, поэтому их концентрация относительно центра сферы определяется исключительно расстоянием до начала координат. Обозначим это расстояние h, тогда от полярных координат можно перейти к линейным и закон Фика в этом случае приобретает вид

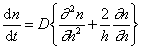, (2.3.141)

или

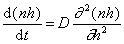. (2.3.142)

Граничные условия интегрирования уравнения (2.3.142) вытекают из соображений, что при t = 0 n = n₀ , если h > R, а при t > 0 n = 0 , если h = R.

Решение уравнения (2.3.139) при граничных условиях имеет вид

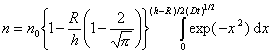. (2.3.143)

В стационарном процессе частичная концентрация n на расстоянии h не зависит от времени коагуляции, поэтому вторым членом в уравнении (2.3.143) можно пренебречь. Тогда уравнение (2.3.143) приводят к виду

n = n₀{ 1 – (R/h)}. (2.3.144)

В стационарном процессе поток частиц к сфере радиуса R, т.е. число всех частиц, которые пересекают поверхность этой сферы за 1 с. согласно первому закону Фика будет

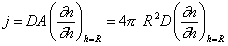, (2.3.145)

где А – площадь поверхности сферы.

Производную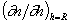 находят дифференцированием уравнения (2.3.144)

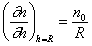. (2.3.146)

Следовательно для диффузионного потока

j = 4pRDn₀. (2.3.147)

Поскольку в реальных условиях ни одну из частиц невозможно сделать неподвижной, то и центральная частица перемещается в пространстве подобно диффундирующим к ней частицам. Поэтому необходимо рассматривать не движение диффундирующих частиц к некоторой неподвижной центральной частице, а относительное движение двух подвижных частиц.

Поскольку частицы перемещаются независимо друг от друга, то постоянная диффузии будет складываться из постоянных диффузии различных частиц, т.е.

D₁₂ = D₁ + D₂. (2.3.148)

Если частицы имеют одинаковый размер, то

D₁₂ =2 D₁ . (2.3.149)

Доказательство справедливости уравнений (2.3.148) и (2.3.149) проводят при рассмотрении относительного среднего сдвига частиц. Из теории броуновского движения известно, что

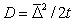, (2.3.150)

где 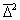- средний квадратичный сдвиг частицы.

Относительное смещение частиц будет

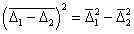. (2.3.151)

Поэтому

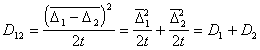. (2.3.152)

Для одинаковых частиц

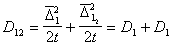. (2.3.153)

Для потока j частиц через сферу радиуса R, движущуюся вместе с одной из них, подставляя вместо D₁₂ =2 D, получаем

j = 8pRDn₀. (10.154)

Поток j выражает скорость агрегирования по отношению к одной частице, для всех n₀ частиц в 1 м³ она будет в n₀ раз больше, следовательно,

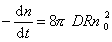(2.3.155)

или

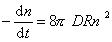, (2.3.156)

так как уравнение (2.3.155) справедливо для любой концентрации частиц в любой момент времени от начала коагуляции.

Таким образом, постоянная скорости коагуляции имеет физический смысл

к = 8pRD . (2.3.157)

Интегрирование уравнения (2.3.156) проводим в пределах от 0 до t и, соответственно, от n₀ до n. В результате интегрирования получаем

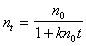. (2.3.158)

Это уравнение может быть использовано для расчета кинетической кривой коагуляции, однако экспериментальное определение постоянной скорости коагуляции встречает определенные трудности. В процессе коагуляции в результате слипания частиц происходит изменение их размера и, следовательно, коэффициента диффузии и радиуса сферы сил притяжения. При этом постоянная скорости коагуляции оказывается связанной с двумя неопределенными величинами. Поэтому кинетическое уравнение приводят к виду, не содержащему постоянной скорости коагуляции.

Прием, который применил Смолуховский, заключается в определении времени половинной коагуляции, когда

n_t =n₀/2. (2.3.159)

Поэтому

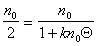, (2.3.160)

где Q – время половинной коагуляции, определяемое по времени, в течение которого начальная частичная концентрация изменится в два раза.

Следовательно

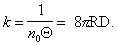(2.3.161)

Подставляя значение постоянной скорости коагуляции из уравнения (2.3.161) в уравнение (2.3.158), получаем

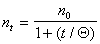. (2.3.162)

Определение постоянной скорости коагуляции можно проводить графическим методом после построения графика в координатах линейной формы уравнения Смолуховского

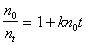. (2.3.163)

В соответствии с этим уравнением постоянную скорости коагуляции можно определить по тангенсу угла наклона, если известна величина начальной частичной концентрации n₀. Пример такой зависимости приведен на рис. 2.25.

В процессе коагуляции в результате слипания частиц происходит изменение их размера и, следовательно, коэффициент диффузии и радиуса сферы сил притяжения. При этом постоянная скорости коагуляции оказывается связанной с двумя неопределенными величинами. Поэтому кинетическое уравнение приводят к виду, не содержащему постоянной скорости коагуляции.

Для расчета концентрации агрегатов частиц любого порядка была получена формула

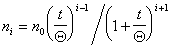, (2.3.164)

где i – порядок, т.е. число соединившихся в агрегат частиц.

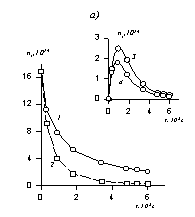
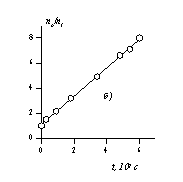
Расчет кинетических кривых по уравнениям (2.3.162) и (2.3.164) приводит к зависимостям, показанным на рис.2.25, а. На рис. 2.25, б приведена кинетическая кривая коагуляции в линейных координатах уравнения Смолуховского (2.3.163), используемая для определения постоянной скорости коагуляции.

Иногда расчеты постоянной скорости проводят теоретически, для чего используют уравнение Эйнштейна, связывающее коэффициент диффузии и размер частиц

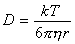, (2.3.165)

где D – коэффициент диффузии, k- постоянная Больцмана, h – вязкость дисперсионной среды, r – радиус частиц.

При выводе выражения для постоянной скорости коагуляции принимаем, что столкновение и слипание частиц происходит при их сближении на расстояние R = 2r, поэтому

D = kT /(3phR) . (2.3.166)

Подставляя уравнение (2.3.166) в выражение для постоянной скорости (2.3.161), получаем

к = 8kT/3h . (2.3.167)

Из этого выражения видим, что постоянная скорости коагуляции не зависит от размеров частиц, а определяется лишь вязким сопротивлением среды и температурой системы.

Для времени половинной коагуляции из уравнений (2.3.161) и (2.3.167) получаем уравнение

Q = 1/кn₀ = 3h/(8 kT n₀). (2.3.168)

Следовательно, время половинной коагуляции также не зависит от свойств частиц, а является функцией начальной частичной концентрации, вязкости среды и температуры.