Теория Мекора
В 1951 г. Мекор предложил в качестве критерия отталкивания между частицами дисперсной фазы рассматривать понижение конформационной энтропии полимерных молекул, адсорбированных на поверхности частиц. В качестве рабочей модели цепей стабилизирующих макромолекул Мекор принял модель жесткого стержня, шарнирно закрепленного на поверхности. Предполагалось, что сближение частиц на расстояния, меньшие длины этих стержней должно приводить к снижению конформационной энтропии (SR), соответственно к изменению энергии Гиббса системы. В качестве математической модели было использовано уравнение
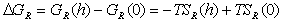, (2.3.54)
где (h) и (0) обозначают соответствующие значения на расстоянии h и в начальном состоянии до перекрытия оболочек стабилизатора.
Изменение конформационной энтропии Мекор находил по уравнению Больцмана
S = k lnW, (2.3.55)
где W – число возможных способов размещения жесткого стержня на поверхности частицы.
Количество конформаций считалось пропорциональным доступному объему при вращении стержня в полусфере радиусом L, равным длине молекулы полимера. Площадь поверхности полусферы, доступная для свободного конца макромолекулы определялась как
A0= 2pL2. (2.3.56)
Если плоские частицы сближаются на расстояние h < L, то эта площадь составит
A(h) = 2p Lh. (2.3.57)
С учетом уравнений (2.3.55)-(2.3.57) уравнение для изменения энергии Гиббса можем записать как
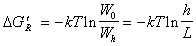. (2.3.58)
Разлагая в ряд логарифмическую функцию в уравнении (2.3.58) при условии, что h » L, ограничиваясь только первым членом разложения, получаем
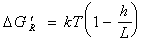. (2.3.59)
Уравнение (2.3.59) позволяет рассчитать изменение энергии Гиббса для одной молекулы. Для единицы площади поверхности частиц с адсорбированными N макромолекулами и степенью заполнения Q запишем
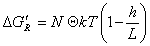. (2.3.60)
Это уравнение позволяет провести приближенный расчет изменения энергии Гиббса при перекрытии адсорбционно-сольватных оболочек. В этой примитивной теории, основанной на предпосылке, что при перекрытии адсорбционно-сольватных оболочек макромолекулы не смешиваются, используется неверная предпосылка о жесткости макромолекул, не способных к изменению своей конформации, и не учитывается сольватация макромолекул, что не позволяет объяснить влияния температуры на устойчивость дисперсных систем, стабилизированных по стерическому механизму. Эти недостатки теории делают её в настоящее время интересной только в историческом плане, а практическое её применение оказалось невозможным.