Электронный парамагнитный резонанс (ЭПР), резонансное поглощение электромагнитной энергии в сантиметровом или миллиметровом диапазоне длин волн веществами, содержащими парамагнитные частицы. ЭПР — один из методов радиоспектроскопии. Парамагнитными частицами могут быть атомы и молекулы, как правило, с нечётным числом электронов (например, атомы азота и водорода, молекулы NO); радикалы свободные (например, CH3); ионы с частично заполненными внутренними электронными оболочками (например, ноны переходных элементов); центры окраски в кристаллах; примесные атомы (например, доноры в полупроводниках); электроны проводимости в металлах и полупроводниках.
ЭПР открыт Е. К. Завойским в 1944. Начиная с 1922 в ряде работ высказывались соображения о возможности существования ЭПР. Попытка экспериментально обнаружить ЭПР была предпринята в середине 30-х гг. нидерландским физиком К. Гортером с сотрудниками. Однако ЭПР удалось наблюдать только благодаря радиоспектроскопическим методам, разработанным Завойским. ЭПР — частный случай магнитного резонанса. Его описание в рамках классической физики состоит в следующем: во внешнем постоянном магнитном поле Н вектор магнитного момента m прецессирует вокруг направления магнитного поля Н с частотой v, определяемой соотношением
2pv = gН. (1)
Здесь g — гиромагнитное отношение. Угол прецессии q (угол между векторами Н и m) при этом остаётся постоянным. Если систему поместить в магнитное поле H1^H, вращающееся вокруг Н с частотой v, то проекция вектора m на направление поля Н будет изменяться с частотой v1 = gH1/2p. Это изменение проекции m с частотой v1 под действием радиочастотного поля H1 (рис. 1) имеет резонансный характер и обусловливает ЭПР. При исследовании ЭПР обычно используют линейно поляризованное переменное магнитное поле, которое можно представить в виде суммы двух полей, вращающихся в противоположные стороны с частотой v. Одна из компонент, совпадающая по направлению вращения с прецессией, вызывает изменение проекции магнитного момента m на Н.
Приведённое классическое рассмотрение удобно для анализа релаксационных процессов (см. ниже). Для описания же спектров ЭПР необходим квантовый подход. Поглощение электромагнитной энергии происходит в том случае, когда квант электромагнитной энергии hv (h — Планка постоянная) равен разности энергий DE между магнитными (зеемановскими) подуровнями, образующимися в результате расщепления уровней энергии парамагнитной частицы в постоянном магнитном поле Н (см. Зеемана эффект).
Если магнитный момент парамагнитной частицы обусловлен только спином электрона S = 1/2, то m = gsbMs, где gs = 2,0023 — фактор спектроскопического расщепления для свободного электрона, b — магнетон Бора, a Ms — магнитное квантовое число, принимающее значения ± 1/2. Во внешнем статическом магнитном поле Н эти электроны парамагнитных частиц разбиваются на 2 группы с энергиями — gsbH/2 и + gsbH/2. Между этими группами уровней возможны квантовые переходы, которые возбуждаются полем H1^H. Условие резонанса записывается в виде:
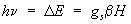 . (2)
. (2)
Это условие эквивалентно условию резонанса (1), т. к. g = 2pgsb/h. Распределение электронов между двумя уровнями энергии описывается формулой Больцмана:
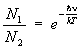 (3)
(3)
где N1 и N2 — числа электронов, находящихся на верхнем и нижнем уровнях, Т— температура, k — Больцмана постоянная. Под действием электромагнитного поля h1 происходит переход электронов с одного уровня на другой, сопровождающийся изменением направления спина.
При переходе с нижнего уровня на верхний электромагнитная энергия поглощается, а при обратном переходе излучается. Вероятность этих процессов одинакова, но т. к. в условиях равновесия населённость нижнего уровня больше, чем верхнего, происходит поглощение энергии (рис. 2). Если каким-либо искусственным образом создать инверсию населённостей, то под действием электромагнитного поля система будет излучать энергию. Этот принцип положен в основу работы парамагнитных квантовых усилителей.
Обычно парамагнетизм частиц обусловлен суммарным вкладом орбитального и спинового моментов нескольких электронов; к тому же в кристаллах на эти электроны действуют сильные электрические поля окружающих ионов (лигандов). Поэтому описание строения спектров ЭПР в этом случае — сложная задача. Для расчёта спектров используют полуэмпирический метод, предложенный А. Абрахамом (Франция) и Х. М. Л. Прайсом (США) в 1951, называемый методом спинового гамильтониана. При ЭПР происходят переходы между близколежащими уровнями. Расчёт уровней энергии в магнитном поле упрощается, если ввести эффективный спин S, абсолютная величина которого определяется числом n близколежащих уровней: n =2S + 1. Энергии вычисляют в предположении, что магнитный момент частицы обусловлен величиной S. Тогда энергия уровня E =gbMsH, где Ms принимает (2S + 1) значений: S, (S — 1),...... — (S — 1), — S. Величина g-фактора может существенно отличаться от величины g-фактора свободного электрона gs. Между уровнями, отличающимися по Ms на величину DMs = ± 1, возможны дипольные переходы, и условия резонанса по-прежнему будут описываться формулой (2) с gs = g. Если S > 1/2, то уровни энергии с разными |Ms| могут расщепиться при Н = 0, и в спектре ЭПР появляется несколько линий поглощения (тонкая структура спектра ЭПР, рис. 3, а).
Взаимодействие электронов с магнитным моментом ядра парамагнитного атома приводит к появлению в спектре ЭПР сверхтонкой структуры. Если спин ядра I, то количество сверхтонких компонент равно 2I + 1, что соответствует условию перехода DMI = 0, где MI — ядерное магнитное квантовое число (рис. 3, б). Взаимодействие электронов парамагнитной частицы с магнитными моментами ядер окружающих ионов также расщепляет линию ЭПР (суперсверхтонкая структура, рис. 4) Изучение сверхтонкого и суперсверхтонкого взаимодействия даёт возможность определить места нахождения неспаренных электронов.
Парамагнитная релаксация. Ширина линий. Релаксационные процессы, восстанавливающие равновесие в системе электронных спинов, нарушенное в результате поглощения электромагнитной энергии, характеризуются временами релаксации T1 и T2. Ширина линий поглощения Dv связана с временами релаксации соотношением:
Dn = (1/ T1) + (1/ T2). (4)
В классическом рассмотрении времена T1 и T2 называются продольным и поперечным временами релаксации, т. к. они определяют время восстановления равновесного положения продольной и поперечной компонент вектора намагниченности. Т. к. восстановление равновесной величины поперечной компоненты намагниченности происходит благодаря взаимодействию между магнитными моментами парамагнитных частиц (спин-спиновое взаимодействие), то T1 называется также временем спин-спиновой релаксации. Восстановление продольной компоненты обусловлено взаимодействием магнитных моментов парамагнитных частиц с колебаниями кристаллической решётки (спин-решёточное взаимодействие). Поэтому время T1 называется также временем спин-решёточной релаксации. Оно характеризует скорость восстановления равновесия между спиновой системой и колебаниями решетки.
Спин-спиновое взаимодействие состоит из двух составляющих: диполь-дипольного и обменного взаимодействий. Локальное поле, действующее на парамагнитную частицу, складывается из внешнего поля Н и поля НД, создаваемого диполями (магнитными моментами) соседних парамагнитных частиц. Поле НД изменяется от точки к точке, т. к. изменяется набор соседних парамагнитных частиц и направление их магнитных моментов, что приводит к уширению линии ЭПР. Обменное взаимодействие, наоборот, стремится упорядочить направления спинов и, следовательно, уменьшает «хаотичность» ориентаций магнитных моментов парамагнитных частиц. Поэтому оно приводит к «обменному сужению» линии ЭПР.
Движения ядер парамагнитных центров создают флуктуации электрического поля, влияющие на орбитальное движение электронов, что, в свою очередь, приводит к появлению флуктуаций локального магнитного поля, а следовательно, и к уширению линий ЭПР. Величина спин-решёточного взаимодействия уменьшается при понижении температуры, т. к. уменьшается амплитуда тепловых колебаний решётки ядер. Величина спин-спинового взаимодействия от температуры практически не зависит. Поэтому для ионов переходных металлов с большим вкладом орбитального момента линию ЭПР удаётся наблюдать только при низких температурах. Спектры ЭПР наблюдают при достаточно малой мощности переменного электромагнитного поля (10-2—10-3 вт), когда установившееся состояние мало отличается от равновесного. Если мощность велика и релаксационные процессы не в состоянии восстановить равновесное распределение, то населённости уровней выравниваются и наступает насыщение, обнаруживаемое по уменьшению поглощения (см. Квантовая электроника). Эффект насыщения уровней используется для измерения времён парамагнитной релаксации.
Экспериментальные методы. ЭПР наблюдается в диапазоне СВЧ. Интенсивность поглощения энергии увеличивается с ростом частоты, т. к. в соответствии с (3) при этом увеличивается различие в населённости уровней. Достаточно высокая чувствительность метода достигается на частоте v = 9000 Мгц. Это соответствует Н = 3200 э (величина магнитного поля, легко получаемая в лабораторных условиях). Использование мощных электромагнитов и сверхпроводящих соленоидов позволяет работать на частотах вплоть до n= 150000 Мгц (длина волны l = 2 мм).
Для измерения поглощения используют радиоспектрометры (спектрометры ЭПР), в которых при постоянной частоте и медленном изменении внешнего магнитного поля регистрируется изменение поглощаемой в образце мощности. В спектрометрах ЭПР прямого усиления высокочастотные колебания от клистрона по волноводному тракту подаются в объёмный резонатор (полость размером ~ l), помещенный между полюсами электромагнита. Прошедшие через резонатор или отражённые от него электромагнитные волны попадают на кристаллический детектор. Изменение поглощаемой в образце мощности регистрируется по изменению тока детектора. Для повышения чувствительности спектрометра внешнее магнитное поле модулируют с частотой 30 гц — 1 Мгц. При наличии в образце поглощения прошедшие или отражённые от резонатора СВЧ-волны также оказываются промодулированными. Промодулированный сигнал усиливается, детектируется и подаётся на регистрирующее устройство (осциллограф или самописец). При этом записываемый сигнал имеет форму производной от кривой поглощения (рис. 4). Чувствительность спектрометра ЭПР определяется уровнем тепловых шумов усилителя. В супергетеродинных спектрометрах на детектор подаётся мощность от дополнительного клистрона. Частота колебаний, генерируемых этим клистроном, отличается от частоты сигнального клистрона. Сигнал с детектора усиливается на разностной частоте 30—100 Мгц.
Применение метода ЭПР. Наиболее хорошо изучены спектры ЭПР ионов переходных металлов. Для того чтобы устранить уширение линии, обусловленное дипольным взаимодействием с соседними парамагнитными ионами, измерения проводят на монокристаллах, являющихся диамагнитными диэлектриками, куда в качестве примесей (0,001%—0,1%) вводят парамагнитные ионы. Влияние окружающих ионов на парамагнитный ион рассматривают как действие точечных электрических зарядов. ЭПР наблюдают на заселённых нижних энергетических уровнях парамагнитного иона, получающихся в результате расщепления основного уровня электрическим полем окружающих зарядов (см. Кристаллическое поле). В случае ионов редкоземельных элементов кристаллическое поле оказывается слабым по сравнению с взаимодействием электронов иона, т. к. парамагнетизм этих ионов обусловлен глубоко лежащими 4 f-электронами. Момент количества движения иона определяется суммой орбитального и спинового моментов основного уровня. В кристаллическом поле уровни с разной абсолютной величиной проекции полного магнитного момента не эквивалентны по энергии. Для ионов группы Fe, парамагнетизм которых обусловлен 3 d-электронами, кристаллическое поле оказывается сильнее спин-орбитального взаимодействия, определяющего энергетический спектр свободного иона. В результате максимальная величина проекции орбитального момента либо уменьшается, либо становится равной нулю. Принято говорить, что происходит частичное или полное «замораживание» орбитального момента.
Симметрия кристаллического поля определяет симметрию g-фактора, а напряжённость кристаллического поля определяет его величину. Поэтому изучение g-фактора парамагнитных ионов позволяет исследовать кристаллические поля. По спектрам ЭПР можно определить также заряд парамагнитного иона, симметрию окружающих его ионов, что в сочетании с данными рентгеновского структурного анализа даёт возможность определить расположение парамагнитного иона в кристаллической решётке. Знание энергетических уровней парамагнитного иона позволяет сравнивать результаты ЭПР с данными оптических спектров и вычислять магнитные восприимчивости парамагнетиков.
Метод ЭПР широко применяется в химии. В процессе химических реакций или под действием ионизирующих излучений могут образовываться молекулы, у которых хотя бы один электрон не спарен (незаполненная химическая связь). Эти молекулы, называются свободными радикалами, относительно устойчивы и обладают повышенной химической активностью. Их роль в кинетике химических реакций велика, а метод ЭПР — один из важнейших методов их исследования; g-фактор свободных радикалов обычно близок к значению gS, а ширина линии мала. Из-за этих качеств один из наиболее устойчивых свободных радикалов (a-дифинил-b -пикрилгидразил), у которого g = 2,0036, используется как стандарт при измерениях ЭПР.
Изучение локализованных неспаренных электронов исключительно важно для исследования механизмов повреждения биологической ткани, образования промежуточных молекулярных форм в ферментативном или другом катализе. Поэтому метод ЭПР интенсивно используется в биологии, где с его помощью изучаются ферменты, свободные радикалы в биологических системах и металлоорганические соединения.
В кристаллах делокализованные электроны и дырки могут захватываться дефектами и примесями, практически неизбежными в кристаллической решётке. Очень часто эти центры определяют окраску кристаллов (см. Центры окраски). Метод ЭПР позволяет по расположению неспаренных электронов определить природу и локализацию центров окраски. В полупроводниках удаётся наблюдать ЭПР, вызываемый электронами, связанными на донорах.
В металлах и полупроводниках наряду с циклотронным резонансом, обусловленным изменением орбитального движения электронов проводимости под действием переменного электрического поля СВЧ, возможен ЭПР, связанный с изменением ориентации спинов электронов проводимости. Наблюдение ЭПР на электронах проводимости затруднительно, т. к.: 1) доля неспаренных электронов проводимости мала (~kT/EF, где EF — Ферми энергия); 2) из-за скин-эффекта глубина проникновения электромагнитного поля в диапазоне СВЧ чрезвычайно мала (~ 10-3—10-6 см); 3) форма линии поглощения сильно искажена из-за скин-эффекта и диффузии электронов.
ЭПР наблюдается в растворах и стеклах, содержащих ионы переходных металлов. Это позволяет судить о заряде парамагнитных ионов, строении сольватных оболочек и т. п. Спектр ЭПР в газах (O2, NO, NO2) сложнее, что связано со спино-орбитальным взаимодействием, вращательным движением молекул и влиянием ядерного спина.
Лит.: Альтшулер С. А., Козырев Б. М., Электронный парамагнитный резонанс соединений элементов промежуточных групп, 2 изд., М., 1972; Абрагам А., Блини Б., Электронный парамагнитный резонанс переходных ионов, пер. с англ., т. 1—2, М., 1972—73; Пейк Д. Э., Парамагнитный резонанс, пер. с англ., М., 1965; Бальхаузен К., Введение в теорию поля лигандов, пер. с англ., М., 1964; Эткинс П., Саймоне М., Спектры ЭПР и строение неорганических радикалов, пер. с англ., М., 1970; Инграм Д., Электронный парамагнитный резонанс в свободных радикалах, пер. с англ., М., 1961; Ингрэм Д., Электронный парамагнитный резонанс в биологии, пер. с англ., М., 1972; Людвиг Дж., Вудбери Г., Электронный спиновой резонанс в полупроводниках, пер. с англ., М., 1964.
В. Ф. Мещеряков.
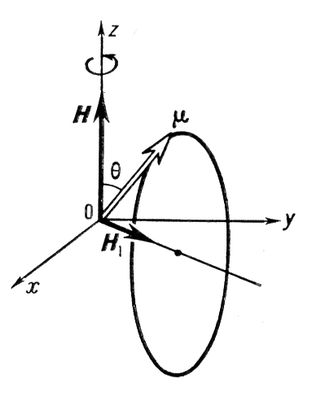
Рис. 1. Изменение угла q прецессии магнитного момента m с частотой n1 = gH1/2p в системе координат охуz, вращающейся вместе с полем H1 вокруг направления Н с частотой n = gH1/2p.
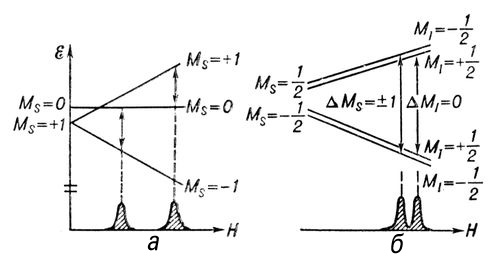
Рис. 3. а — тонкая структура спектра ЭПР. Для случая S = 1 наблюдаются две линии поглощения в результате расщепления уровней при Н = 0; б — сверхтонкая структура спектра ЭПР.
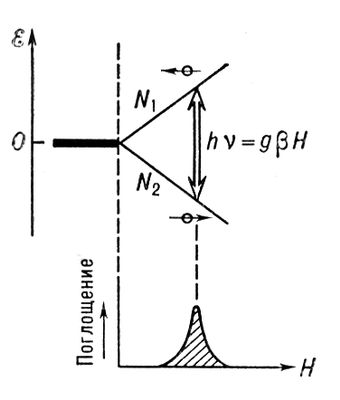
Рис. 2. При hv = g?H происходит резонансное поглощение энергии переменного электромагнитного поля.
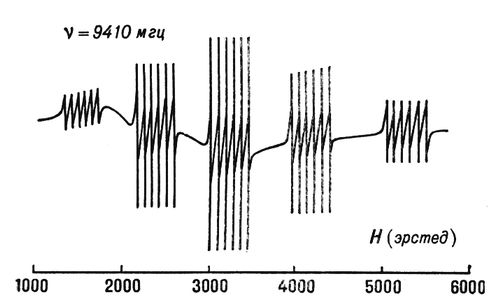
Рис. 4. Спектр ЭПР иона Mn2+ в кристалле метасиликата. Видны 5 групп линий тонкой структуры, соответствующих спину иона Mn2+ S = 5/2. Каждая группа состоит из 6 линий сверхтонкой структуры, обусловленной взаимодействием с ядерным спином I = 5/2.